Visual Angle

Estimated reading time: 6 minutes

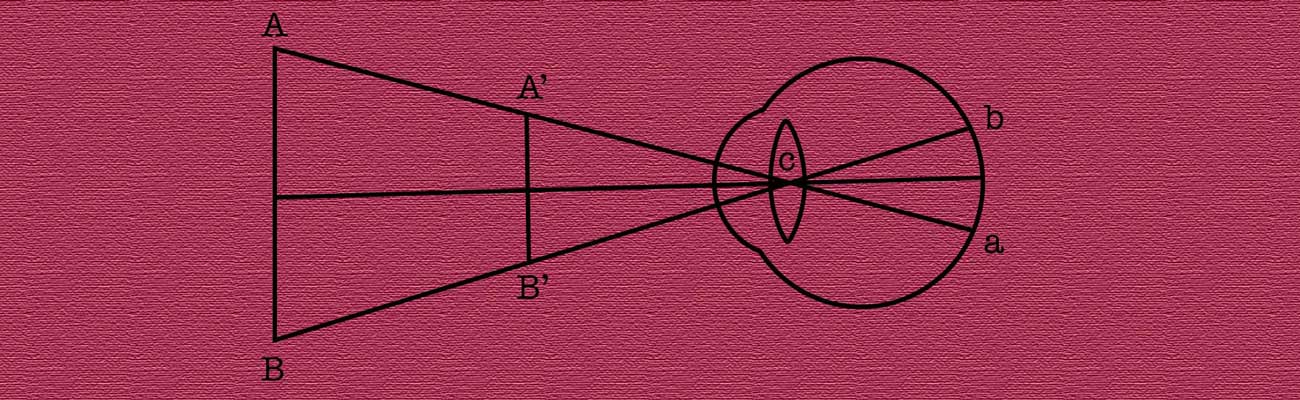
The concept of visual angle is critical to many aspects of eye-tracking research, but it is one of those things that people are somehow just expected to understand. This blog is my attempt to explain visual angle in the way I wish someone had explained it to me, e.g., with the bare minimum of math… And don’t worry, you can avoid the math entirely with this very helpful online app a colleague built!

Why Visual Angles are Important for Eye Tracking

Visual angles are everywhere in eye tracking. Researchers may want to ensure that their screen fits within the “trackable range” of their system – where the trackable range is 32 degrees horizontally and 25 degrees vertically for example. Other researchers may want to ensure that stimuli on screen subtend exactly 5 degrees of visual angle, or that saccade targets appear at +/- 10 degrees of visual angle from the screen center. While the gaze data from eye trackers is generally reported in screen pixel co-ordinates, important metrics such as saccade amplitude and velocity are reported in degrees of visual angle / degrees per second. Also, gaze data is often parsed into saccades and fixations based on the eye’s velocity – which is measured by eye trackers in degrees per second. Finally, many critical measures of eye tracking data quality (and eye tracker specifications) such as “accuracy” and “precision” are reported in degrees of visual angle. For example the EyeLink 1000 Plus is accurate to < 0.5 degs of visual angle.

Clearly, a basic understanding of the concept of visual angle (and being able to convert between screen pixels and degrees of visual angle) can be very helpful in eye tracking research! The basic idea is illustrated below (in the vertical dimension). The visual angle (θ) subtended by the flower is indicated by the purple double headed arrow.

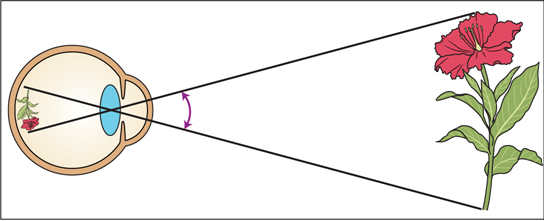
Visual Angle Calculation

Calculating the amplitude of this angle involves some very basic maths – specifically some right-sided triangle trigonometry. You were probably taught this stuff in school – I remember thinking it could never possibly be useful in real life… As you can see in the images below (which switch to the horizontal axis), calculating the visual angle involves doing the sums for one or two right triangles, depending on exactly what it is you want to know. 

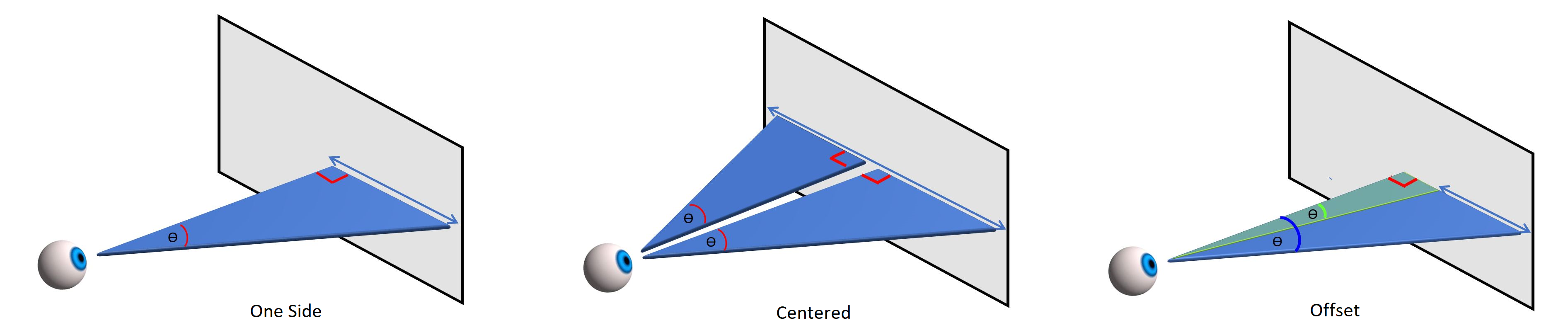
To calculate the visual angle of a target measured from the screen center (e.g if presenting targets at +/- 10 degrees), there is just one right triangle involved. To determine the visual angle subtended by an object that centered on screen (or the visual angle subtended by the screen itself) there are two right triangles, side by side. There are also two right triangles if you want to determine the angle subtended by an object that is offset from the center of the screen. In this case the triangles overlap, and the visual angle of the offset object is the angle of the green triangle subtracted from the angle of the blue triangle.

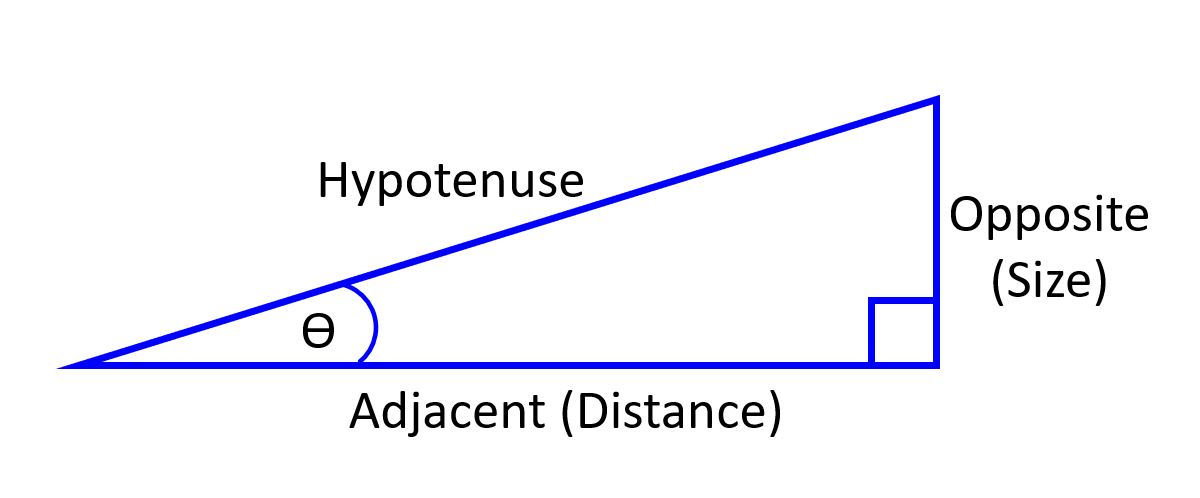
In each case the math is the same – we need to find the angle(s) between the “Opposite” and “Adjacent” sides of the triangle(s) (the long side is the Hypotenuse). In the images above, the Opposite side can be thought of as “size” and the adjacent side can be thought of as “distance”. The ratio of the Opposite and Adjacent edges is tan (remember SOHCAHTOA?). So to find the angle, we just use the inverse tan function (also knows as atan) – θ = atan(Opposite / Adjacent) or θ = atan(Size / Distance).

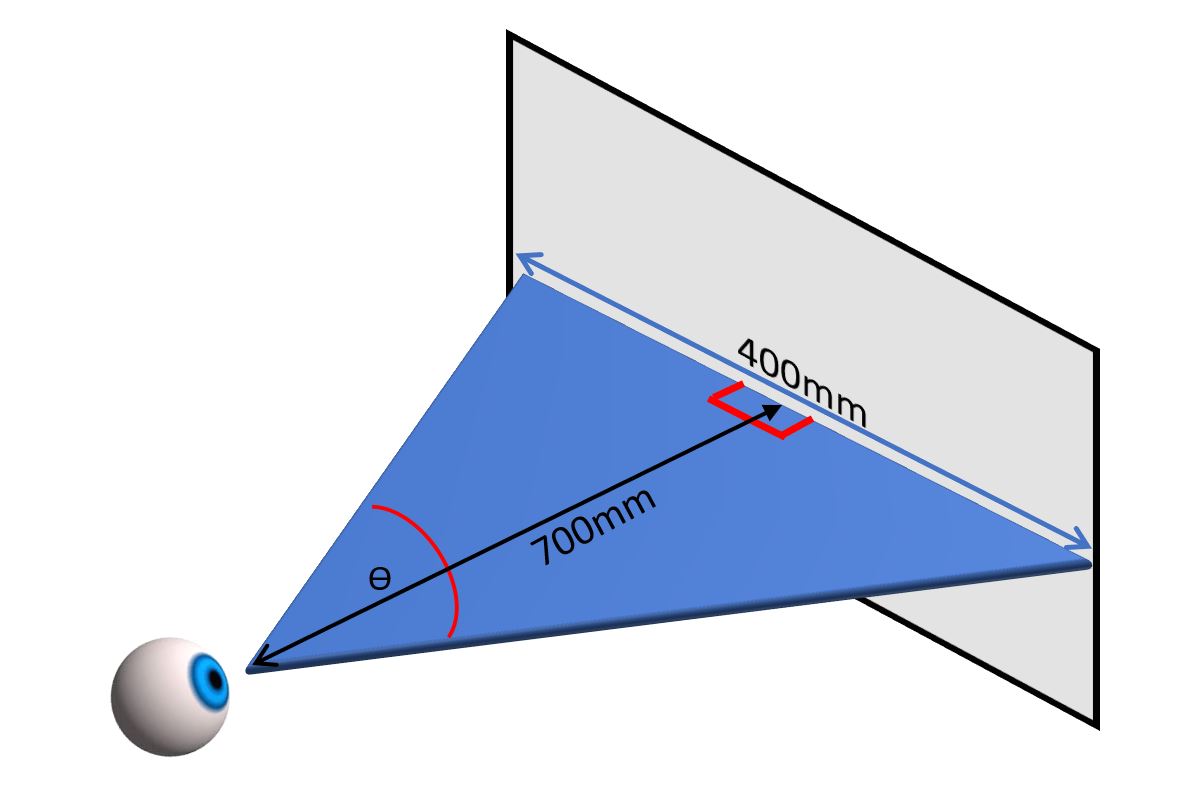
So armed with this knowledge, we can easily compute visual angle simply by measuring the distance (Adjacent) and size (Opposite) of any object being viewed. The simple formula for a single right triangle – θ = atan (Size/Distance) can easily be adjusted to take into account the fact that two right triangles are involved for centered objects – θ = 2*atan(Size/2*Distance). In the image below, the screen is 400mm wide, and 700mm distant. So it subtends 2*atan(400/(2*700)) = 31.9 degrees.

Converting Pixels to Degrees of Visual Angle

Now that we can compute visual angle for objects that can be measured in mm, it is a relatively simple step to move between mm and screen pixels. If we know our screen pixel resolution (e.g. 1920×1080) as well as its dimensions (height and width in mm) it is very easy to work out how many pixels there are per mm. For example, in the horizontal direction, a screen with 1920 pixels, that measures 520mm wide, has 1920/520 = 3.89 pixels per mm. Another way of looking at things is to say that each pixel on the screen is 520/1920 = 0.27mm wide.

This conversion factor allows us to easily switch between pixels and mm, so we can also compute degrees of visual angle based on screen pixels. For example, a target presented 300 pixels to the right of the center of the screen described above is at θ = atan((300*0.27)/700) = 6.6 degrees from the center.

An Online Visual Angle Calculator!

Whilst the math for calculating degrees of visual angle isn’t too tricky (once you’ve got the hang of it), it is much easier to let a computer do it all for you – which is why my colleague Jono from the support team created this handy online visual angle calculator – just enter your screen resolution, dimensions, and distance, and it will convert between pixels and degrees of visual angle for you! Check it out – you can find it and a couple of other handy apps on the “Useful Apps” page.

Contact

If you would like us to feature your EyeLink research, have ideas for posts, or have any questions about our hardware and software, please contact us. We are always happy to help. You can call us (+1-613-271-8686) or click the button below to email:

Read More